Bloom Filters Explained
Bloom filters explained
Background
We use data structures like the HashSet where we can confirm weather an item is present. For the data set with smaller size, confirming membership can be quick but to test if an item is a member of a large dataset can be expensive. The time complexity and space complexity can be linear in the worst case.
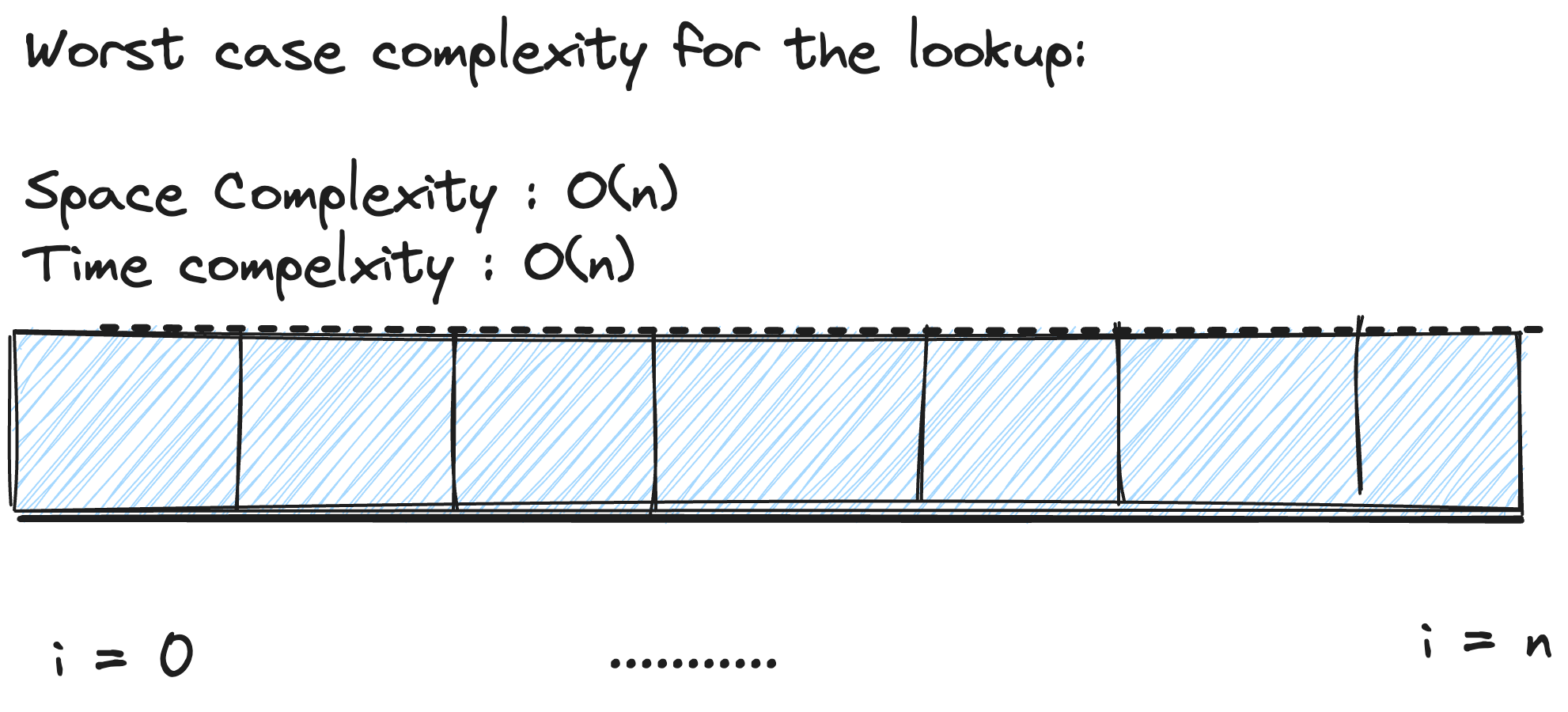
HashMap lookups
This brings us to the need to designing a data structure which fulfils the following cases:
- constant time to test membership
- small memory to test membership
- supports parallel inserts and queries
- approximate membership test
What is a bloom filter?
A bloom filter[1] is probabilistic data structures which offer constant time complexity and constant space complexity. This efficient lookup is provided with a caveat of probabilistic results in nature. Which means, it will always return true if an item is a set member, but it might return true for a lookup even if an item is not a member of the set (false positive case)
Operations supported by a bloom filter:
- insertion (items can only be added but can not be removed)
- test the membership of an item in the set.
How does a bloom filter work?
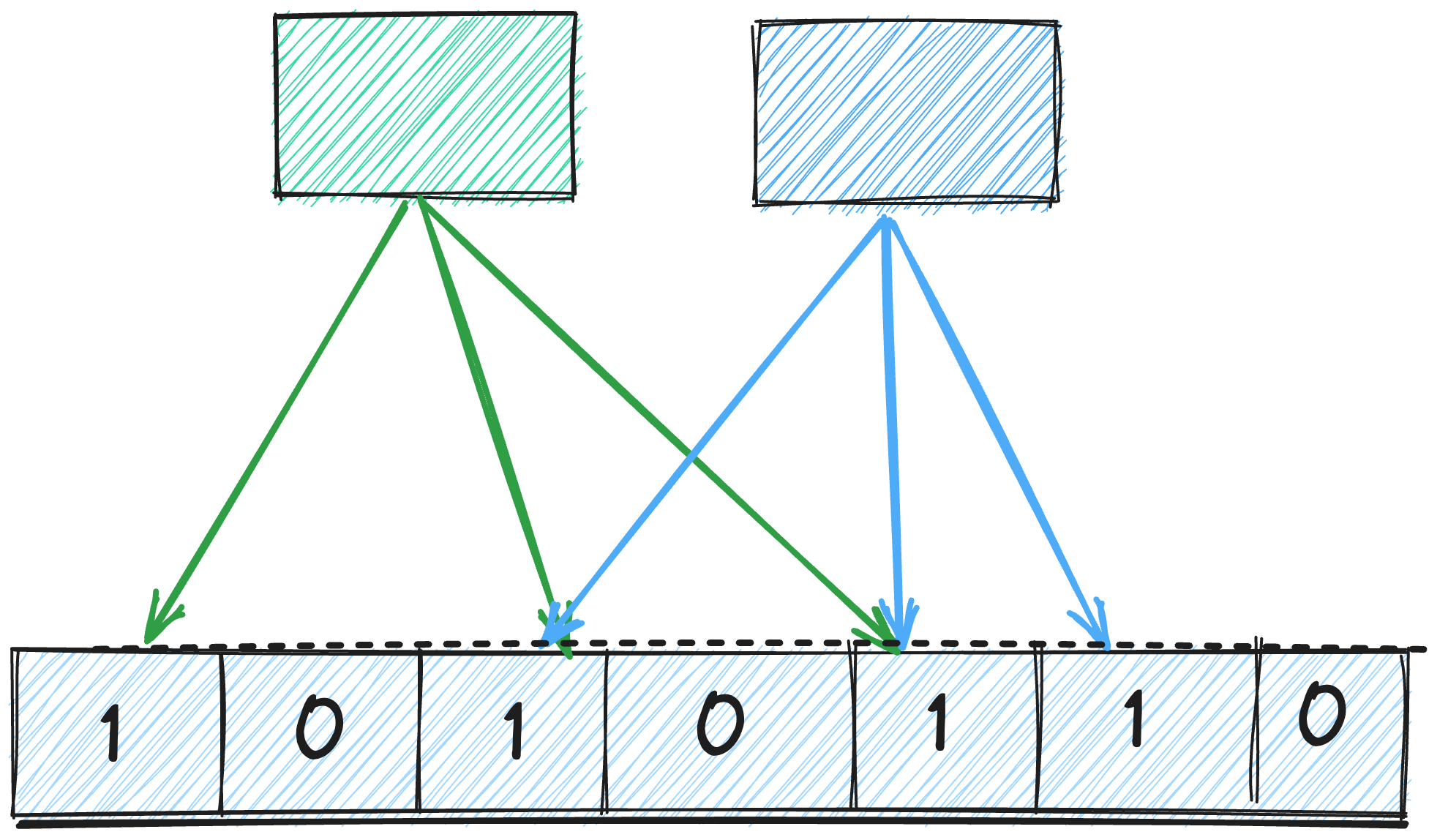
A bloom filter is based on hashing and is very much like a hash table in that it will use a hash function to map a key to a bucket.
It can be visualised as a bit array of length n. The indexes of the bit array (0 to n-1) represents the bucket.
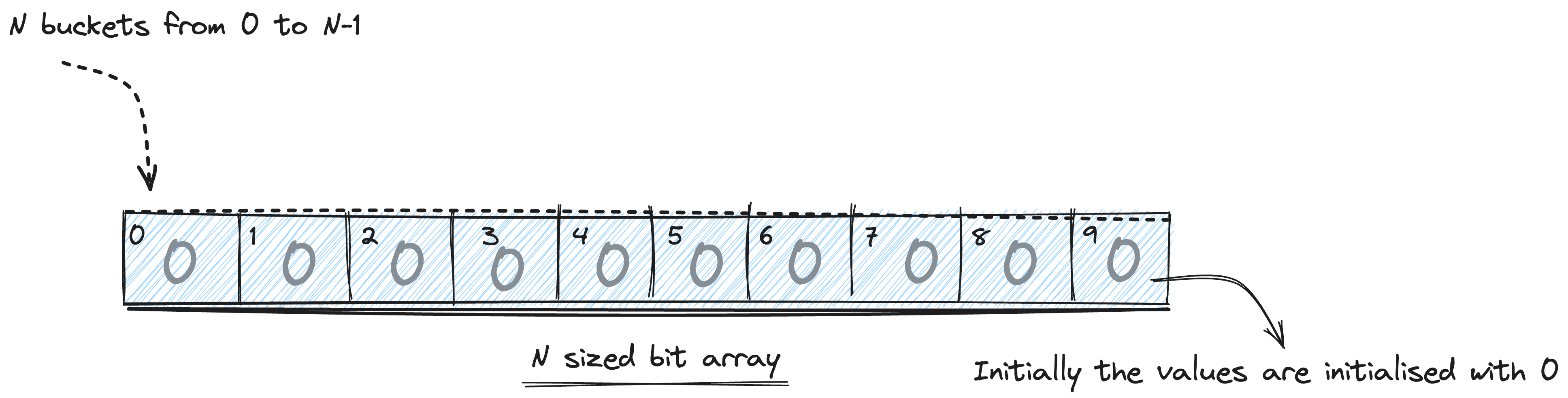
Bloom filter initialisation
Initially all the values are set to 0 when an empty bloom filter is initialised. The values of the items are themselves are not added to a set, instead a hash of the elements (represented by set of bits) is added to the set.
Insertion in the Bloom filter
TLDR; incoming item —> [k hash functions] —> hash % n —> k array positions —> bits in all the identified buckets are set to 1
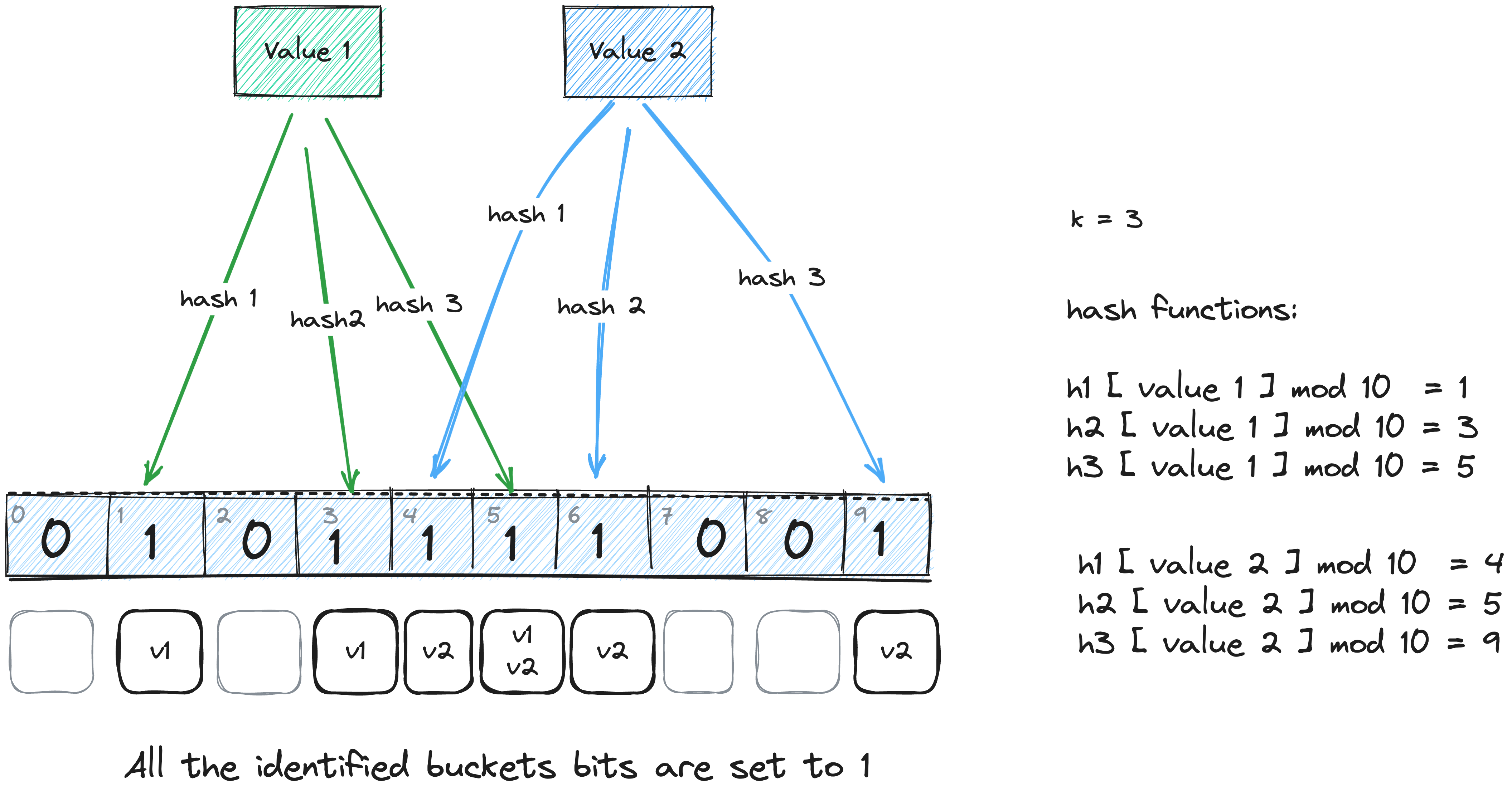
Bloom filter insertion
Any value which has to be inserted to the bloom filters are hashed through k hash function which are independent of each other.
Once we have the hash value, we take modulo with the length of bit array to identify the bit array index (this can also be considered the k positions of values) however it is also possible that some bits on the array are set to one multiple times due to hash collisions.
Membership lookups in the bloom filter
TLDR;
candidate value —> [k hash functions] —> hash % n —> k array positions —> verify if all the bits at identified buckets are 1.
Notable points:
- If any of the identified bits are set to 0, the item is not a member of the bloom filter.
- if all the identified bits are set to 1, the item might be a member of the bloom filter.
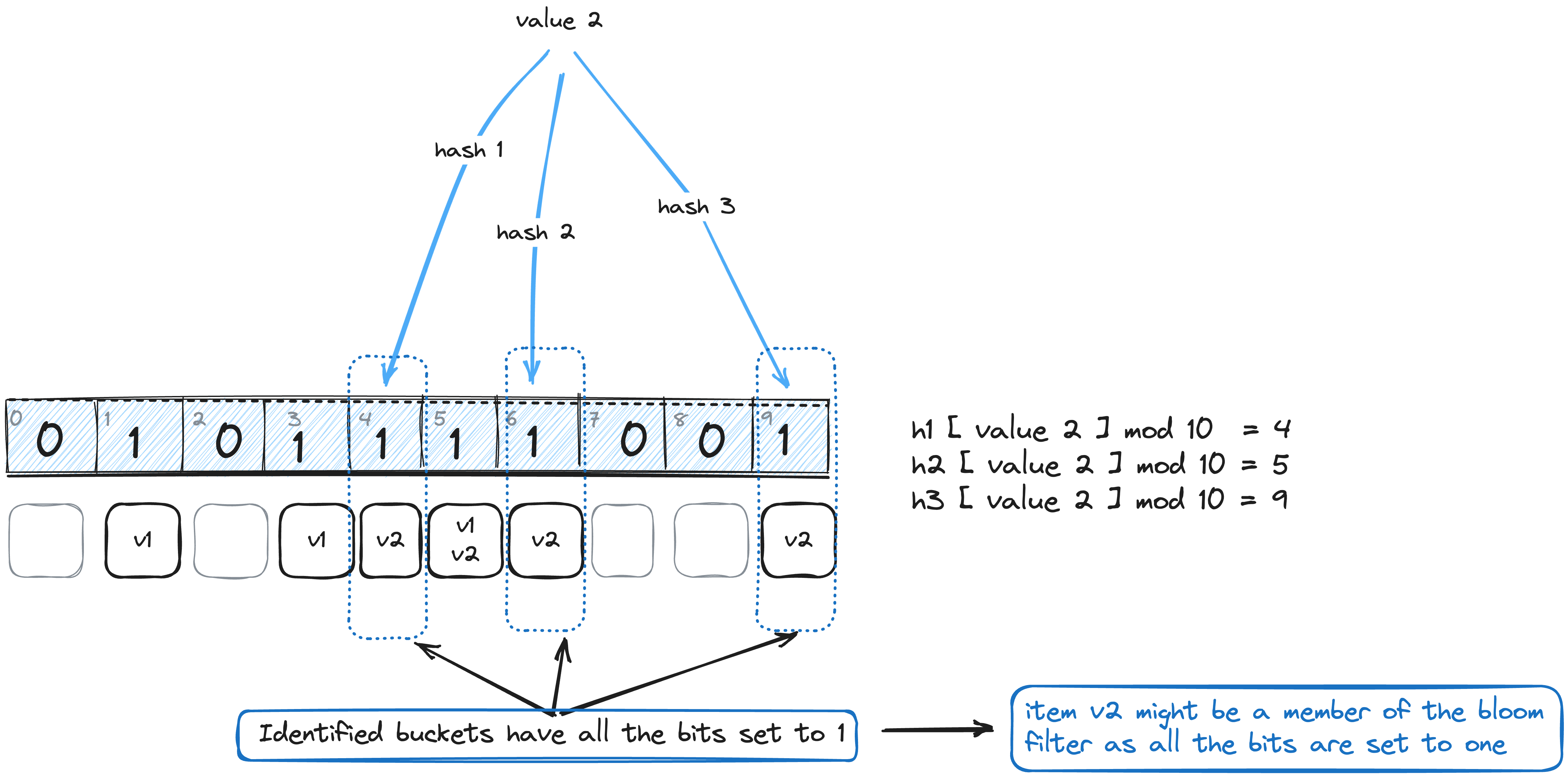
Bloom filter non determinstic lookups
The uncertainty about the membership of an item is due to the possibility of some bits being set to one by different items or due to hash function collisions.
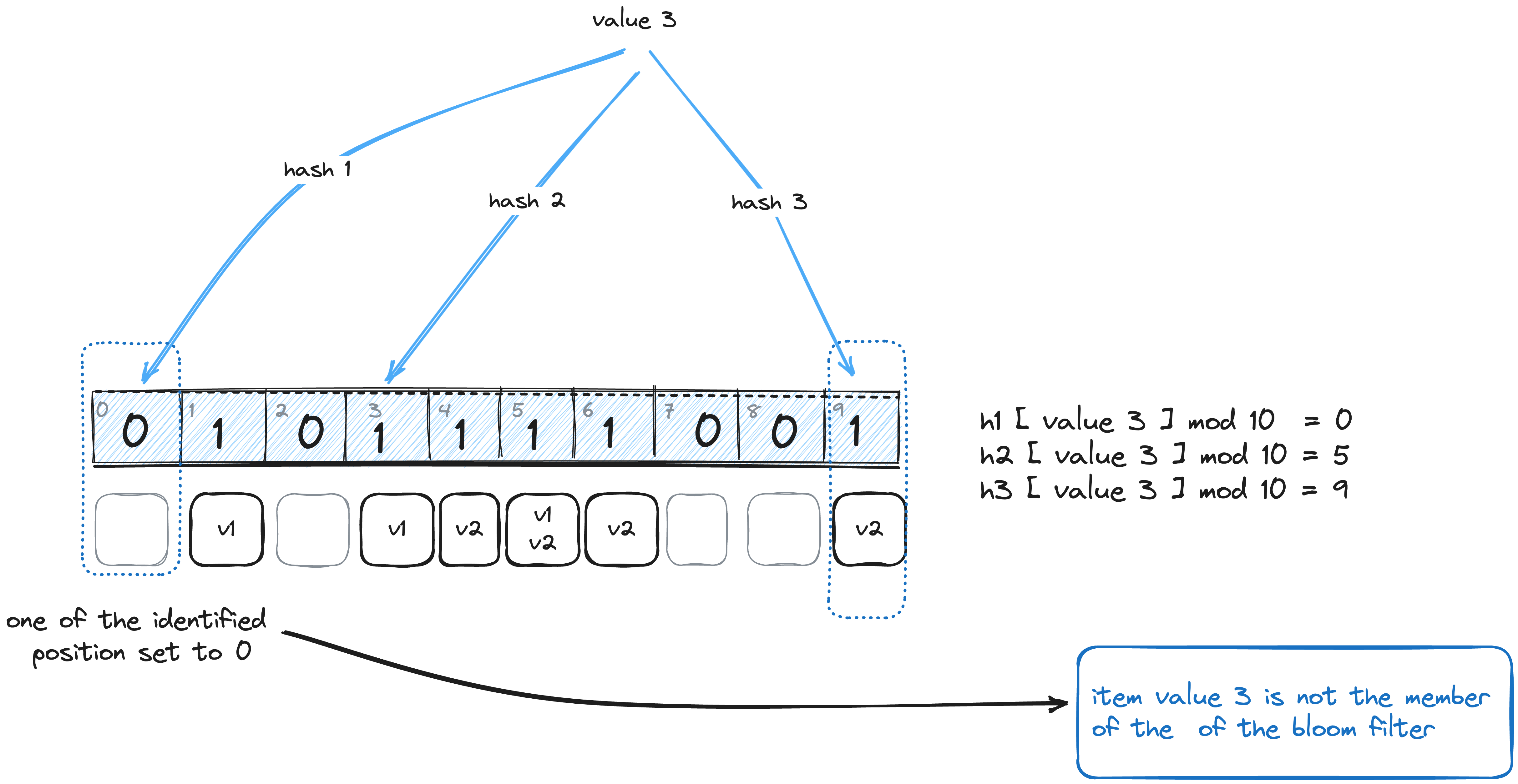
Bloom filter deterministic absence
Bloom filter false positive cases:
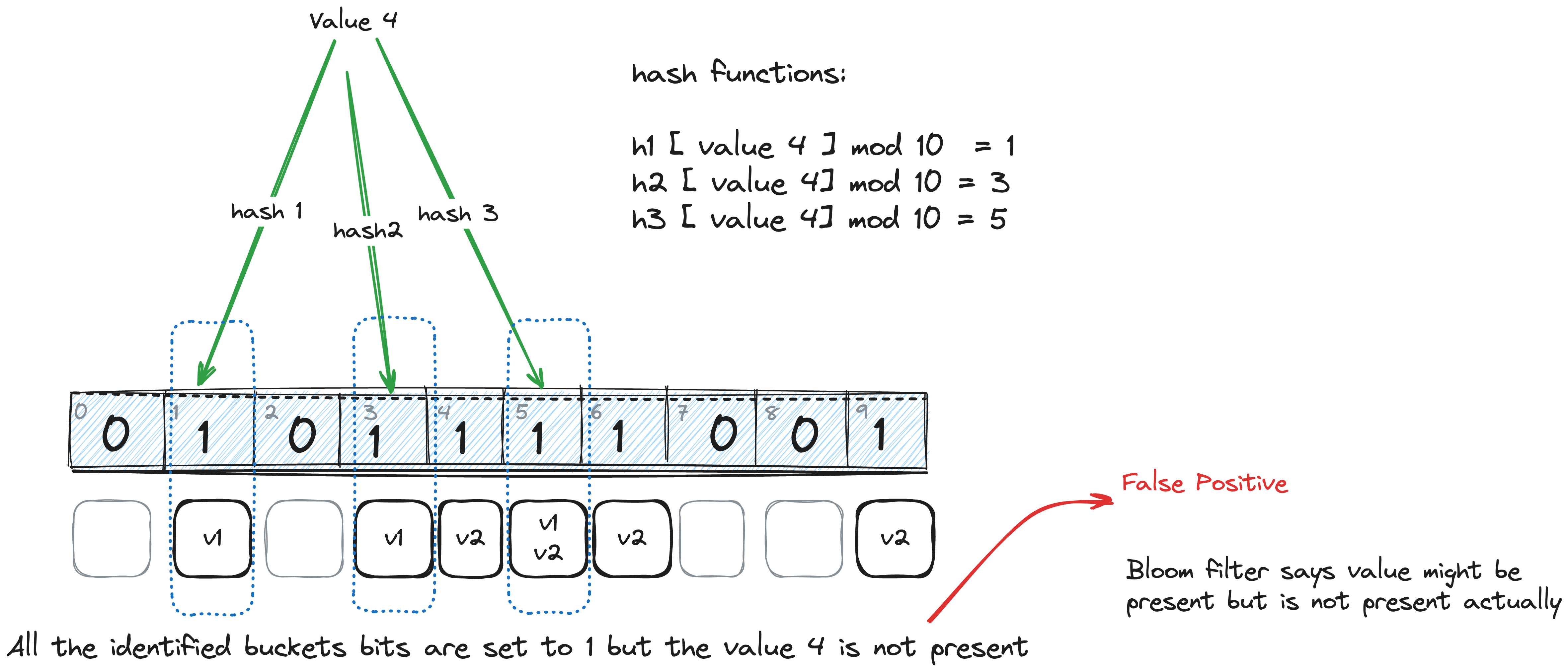
Bloom Filter false positives
It is possible that the same hash functions and modulo can give us bucket positions which have bits set to 1 even if the element is not present in the bloom filter. This is a false positive case.
Asymptotic complexity analysis
A bloom filter is extremely efficient in both time and space usage such that trade off with accuracy is still favourable.
Time
If we are using a bloom filter with n bits and k hash function, insertion and search will both O(k) time.
In both cases, we just need to run the input through all of the hash functions. Then we just check the output bits.
| Operation | Complexity |
|---|---|
| insertion | O(k) |
| search | O(k) |
Note that this is one of the few data structures whose time complexity does not at all depend on the number of elements in it. This is because the elements never really enter the structure, only their hashes are maintained the bit arrays.
Space
To grasp the space complexity of the bloom filter, you must begin by selecting your parameters. You can create a bloom filter with k=1, which would essentially function as a hash table disregarding collisions. Yet, when dealing with a large value of n, particularly when aiming for a low false positive rate, the data structure's space, where the data is stored, becomes O(n).
| Complexity | |
|---|---|
| space | O(n) |
Advantages of bloom filter
There are many advantages of the bloom filters including the complexity which we have just analyzed
- Constant time and space complexity
- Operations are parallelizable
- No false negative cases.
Limitations of the bloom filters
Like the advantages, there are few limitations as well, such as
- Delete operation is not supported because the actual value is not stored, and no possibility to identify the bits that should be cleared once inserted.
- False positive cases (although can be minimised)
Bloom filters use cases:
The bloom filters are useful in high-ingestion systems to prevent expensive disk seeks. The bloom filter in memory can be used to serve the lookups and reduce the unnecessary disk I/O except when the bloom filter returns a false positive.
- The BloomIndexComponent (built with bloom filter) in Solr enables a fast and memory efficient membership test of an element in a read only set.
- Databases use it to avoid disk lookups for non existing keys.
- Past recommendations are avoided being shown by recommender engine.
- MapReduce uses the bloom filter for the efficient processing of large datasets
Implementing Bloom filters with Python:
import hashlib
class BloomFilter:
def __init__(self, m, k):
self.m = m
self.k = k
self.data = [0] * m
self.n = 0
def _hash(self, element, seed):
h = hashlib.md5(element.encode()).hexdigest()
return hash(h[:6]) % self.m
def insert(self, element):
hashes = [self._hash(element, i) for i in range(self.k)]
for hash_value in hashes:
self.data[hash_value] = 1
self.n += 1
def search(self, element):
hashes = [self._hash(element, i) for i in range(self.k)]
for hash_value in hashes:
if self.data[hash_value] == 0:
return f"Searched Key: {element} not in Bloom Filter"
prob = (1.0 - ((1.0 - 1.0 / self.m) ** (self.k * self.n))) ** self.k
return f"Searched Key: {element} might be in Bloom Filter with false positive probability {prob:.10f}"
if __name__ == "__main__":
print("Initialising Bloom Filter with M = 10 and k =2")
bf = BloomFilter(10, 2)
print(f"Initial bloom filter: {bf.data}")
bf.insert("test_value")
print(f"Bloom filter after insertion: {bf.data}")
result = bf.search("test_value")
print(result)
We can check how the bits are flipped once an item is inserted.

Running Bloom filters with Python
Ref:
- Bloom filters on Wikipedia: https://en.wikipedia.org/wiki/Bloom_filter
- False Positive: https://en.wikipedia.org/wiki/False_positives_and_false_negatives#False_positive_error
- Mapreduce: https://en.wikipedia.org/wiki/MapReduce